Fuerzas centrífuga y centrípeta

La fuerza centrífuga y centrípeta son partícipes del movimiento circular, cuya diferencia principal radica en el marco de referencia desde el que se analiza el movimiento.

Fuerza centrifuga

A la fuerza centrífuga se la conoce como pseudo-fuerza o fuerza ficticia, porque no es el resultado de una interacción verdadera entre dos objetos, aunque sea muy real para los ocupantes de un automóvil que está dando una curva, sobre todo si van a buena velocidad. Los pasajeros sienten que algo invisible los empuja hacia afuera, de allí la denominación de fuerza centrífuga, pero en realidad lo que sienten las personas es la inercia que todos los cuerpos poseen: la resistencia natural a cambiar el movimiento. No es posible identificar al agente responsable de “echar fuera” a los pasajeros y por eso la fuerza centrífuga es una fuerza ficticia.

El calificativo de «centrífuga» significa que ‘huye del centro’. En efecto, un observador no inercial situado sobre una plataforma giratoria siente que existe una «fuerza» que actúa sobre él, que le impide permanecer en reposo sobre la plataforma a menos que él mismo aplique otra fuerza dirigida hacia el eje de rotación. Así, aparentemente, la fuerza centrífuga tiende a alejar los objetos del eje de rotación.

En general, la fuerza centrífuga asociada a una partícula de masa

Por lo tanto, el módulo de esta fuerza se expresa por:

Fuerza centrípeta

Se conoce como fuerza centrípeta a la fuerza o al componente de la fuerza que actúa sobre un objeto en movimiento que pasa por una trayectoria curvilínea y que está dirigida hacia el centro de curvatura de la trayectoria.

El término «centrípeta» proviene de las palabras latinas centrum, «centro» y petere, «dirigirse hacia», y puede ser obtenida a partir de las Leyes de Newton. En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.

Los objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por:

Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa m, en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:

Fuerza centrípeta frente a fuerza centrífuga

La «fuerza centrípeta»es la componente de fuerza dirigida hacia el centro de curvatura de la trayectoria de una partícula. En mecánica clásica, las fuerzas centrípetas son fuerzas reales asociadas causalmente a la acción de algún agente exterior a la partícula o el cuerpo. En el caso del movimiento circular uniforme, la fuerza centrípeta está dirigida hacia el centro de la trayectoria circular y es necesaria para producir el cambio de dirección de la velocidad de la partícula. Si sobre la partícula no actuase ninguna fuerza, se movería en línea recta con velocidad constante.

La «fuerza centrífuga» no es una fuerza en el sentido usual de la palabra, sino que es una fuerza ficticia que aparece en los sistemas referenciales no-inerciales. Es decir, la fuerza aparente que un observador no inercial parece percibir como resultado de la no inercialidad de su sistema de referencia.

Así, por ejemplo, si un cuerpo está girando alrededor de un centro de fuerzas fijo, la única fuerza real que actúa sobre el cuerpo es la fuerza de atracción hacia el centro de la trayectoria (fuerza centrípeta) necesaria, desde el punto de vista de un observador estacionario (inercial, [X,Y,Z]) para que el cuerpo pueda describir una trayectoria curvilínea.

Dicha fuerza real, F_cp, (la tensión de la cuerda en el ejemplo ilustrado en la Figura) proporciona la aceleración centrípeta característica de todo movimiento curvilíneo.

Sin embargo, un observador situado en un referencial en el cual el cuerpo esté en reposo (referencial en rotación [x,y,z] y, por tanto, no inercial) observará que el cuerpo no presenta aceleración alguna en la dirección de la fuerza aplicada F_cp (que podrá medir intercalando un dinamómetro en la cuerda de la Figura). Para reconciliar este resultado con el requerimiento de que la fuerza neta que actúa sobre el cuerpo sea nula, el observador imagina la existencia de una fuerza igual y de sentido opuesto a la fuerza centrípeta; esto es, postula la existencia de una fuerza centrífuga, Fcf que no tiene existencia real y que solo resulta útil al observador no-inercial para poder escribir la segunda ley de Newton en la forma usual.

Pongamos otro ejemplo para aclarar el concepto. Imaginemos un pasajero en un automóvil que toma una curva cerrada hacia la izquierda con una cierta velocidad. La inercia asociada a la masa del pasajero se opone a cualquier cambio de dirección de movimiento de este, induciéndole a continuar su inicial trayectoria rectilínea. Puesto que el automóvil gira hacia la izquierda, el pasajero se siente desplazado hacia la puerta situada a su derecha. Una vez que el pasajero establece contacto con la puerta, ésta ejercerá sobre el pasajero la fuerza centrípeta necesaria para que, al igual que el automóvil, pueda girar hacia la izquierda.

El rozamiento entre el asiento y los pantalones del pasajero también contribuye a contrarrestar el efecto centrífugo y, si el viraje se produce a baja velocidad, puede ser suficiente para impedir que el pasajero se deslice sobre el asiento y proporcionar la fuerza centrípeta necesaria para el viraje.

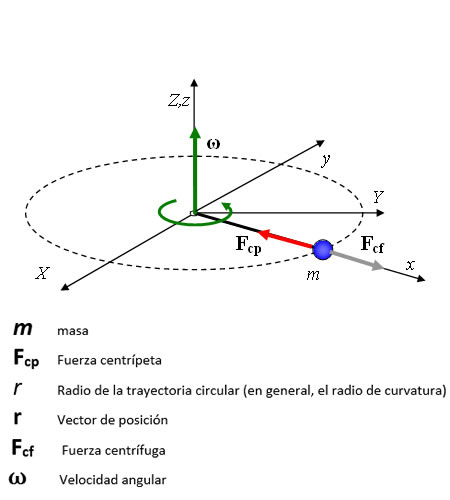
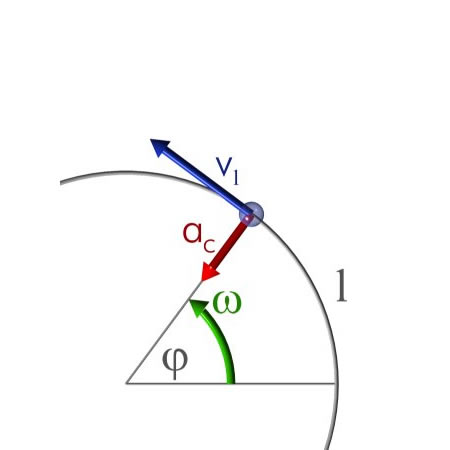Fuerza centrípeta en un movimiento circular