Movimiento parabolico
El movimiento parabólico es el desplazamiento realizado por cualquier objeto cuya trayectoria describe una parábola, el cual corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que presenta mínimos de resistencia durante su avance y que está sujeto a un campo gravitatorio ambos de tipo uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical.
¿Qué es una parábola?
Al lanzar un proyectil este saldrá disparado por el aire formando un arco hasta caer de nuevo al suelo, su trayectoria no es recta, ni circular y menos curvilínea. A esta curva que realiza el proyectil se le llama parábola y se caracteriza por tener un ángulo de salida, uno de llegada y un “eje focal”, que es una línea que se puede trazar justo en la mitad de la curva para confirmar que ambos lados de la parábola son exactamente iguales.
Características de una parábola:
- Sobre el eje focal se ubica un punto fijo llamado "foco", que es el punto de referencia más importante.
- Cualquier punto que ubiques en alguna parte de la parábola, por ejemplo, en el lado derecho, encontrará un punto igual en el lado izquierdo. Lo ideal es que ambos puntos se encuentren a la misma distancia del foco.
Movimiento parabólico
Ahora que ya sabes qué es una parábola y cómo puedes identificarla pasemos a la definición del movimiento parabólico, que en pocas palabras es aquel en el que un objeto se desplaza mientras su trayectoria forma una parábola en el aire. Por ejemplo:
- Una pelota de fútbol que es pateada en un tiro libre.
- Una flecha que sale disparada en el tiro al arco.
- El agua que sale de las mangueras de los bomberos.
Este movimiento también es conocido como “movimiento de proyectiles”.
Características del movimiento parabólico
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical. El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales).
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijada, el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
- La componente horizontal se mantiene constante.
Tipos de movimiento parabólico
Existen diferentes tipos de movimiento parabólico dependiendo desde donde empieza o acaba el movimiento del cuerpo.
- Movimiento parabólico completo: el cuerpo recorre una parábola completa, empezando y acabando en el suelo.
- Movimiento de media parábola (o tiro parabólico horizontal): el cuerpo empieza el movimiento desde cierta altura y es lanzado parabólicamente con una fuerza horizontal, en un punto que sería el punto más alto de la parábola completa ideal.
- Otros movimientos parabólicos: existen muchos casos particulares del movimiento parabólico, por ejemplo el lanzamiento de una pelota desde el suelo a la terraza de una casa o el lanzamiento a canasta de un jugador de baloncesto. Siempre son tramos de una teórica parábola completa.
Ecuaciones
Debido a que el movimiento parabólico, es un ejemplo de composición de movimientos en dos dimensiones: un m.r.u. en el eje horizontal y un m.r.u.a. en el eje vertical. veremos sus ecuaciones:
Las ecuaciones del m.r.u. para el eje x
Las ecuaciones del m.r.u.a. para el eje y
Posición (m)
- Eje horizontal
X = Vx . t = V0 .cos(α).t
- Eje vertical
y = H + V0y .t - 0,5 .g.t2 = H + V0. sin(α).t- 0,5 .g.t2
Velocidad (m/s)
- Eje horizontal
Vx= V0x = V0 .cos(α)
- Eje vertical
Vy= V0y - g .t = V0 .sin(α) - g.t
Aceleración (m/s2)
- Eje horizontal
ax = 0
- Eje vertical
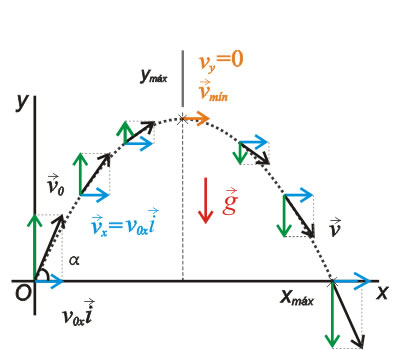 Movimiento parabólico
Movimiento parabólicoDiferentes fuerzas presentes en un movimiento parabólico donde puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical.
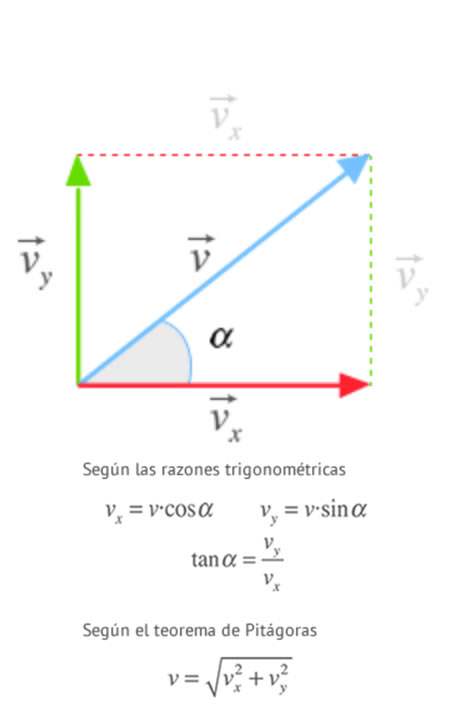 Descomposicion del vector velocidad en el movimiento parabólico
Descomposicion del vector velocidad en el movimiento parabólicoCualquier vector, incluida la velocidad puede descomponerse en 2 vectores que tienen la dirección de los ejes cartesianos X e Y . Los módulos de ambos vectores pueden calcularse a partir del ángulos que crea el vector con la horizontal mediante las expresiones que aparecen en la figura.
