Sistema de referencia Descripción del movimento La velocidad Movimiento rectilíneo y uniforme (MRU) Aceleración Movimiento Uniformemente Acelerado (MUA) Aceleración de la gravedad Movimiento circular uniforme (M.C.U.) Fuerzas centrífuga y centrípeta Movimiento parabolico Movimientos periódicos

La aceleración de la gravedad

Todos los cuerpos caen sobre la superficie de la terrestre con la misma aceleración, independientemente de cual sea su masa. 

Caída libre

Se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a estas como caídas libres, aunque los efectos de la densidad del medio no sean por lo general despreciables. En la caída libre ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en el vacío. En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración, g, que es la aceleración de la gravedad

Las ecuaciones que rigen el movimiento de caida libre son las mismas que las de cualquier movimiento rectilíneo uniformemente acelerado, pero se han de introducir las dos características de este movimiento donde la aceleración es igual a la gravedad a= g = 9,8m/s2 y V0=0 porque el cuerpo comienza desde el reposo y comienza a caer.

Introducimos estos dos valores en la definición de la aceleración y entonces:

v=v0+a*t à v=0+g*t à v=g*t àv= 9,8 m/s2* t

Si hacemos lo mismo con la ecuación del espacio, obtendremos:

s = v0*t+ *a*t2 à  s = 0*t + *g*t2 à s= *g*t2

Las ecuaciones de la caída libre son:


Donde:

  • y: La posición final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro (m)
  • v: La velocidad final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro  (m/s)
  • a: La aceleración del cuerpo durante el movimiento. Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado(m/s2).
  • t: Intervalo de tiempo durante el cual se produce el movimiento. Su unidad en el Sistema Internacional (S.I.) es el segundo (s)
  • H: La altura desde la que se deja caer el cuerpo. Se trata de una medida de longitud y por tanto se mide en metros.
  • g: El valor de la aceleración de la gravedad que, en la superficie terrestre puede considerarse igual a 9.8 m/s2

Ejemplo

Un vaso de agua situado al borde de una mesa cae hacia el suelo desde una altura de 1.5 m. Considerando que la gravedad es de 10 m/s2, calcular:

a) El tiempo que está el vaso en el aire.
b) La velocidad con la que impacta en el suelo.

Solución
Cuestión a)

Datos

  • H = 1.5 m

Cuando llegue al suelo y = 0 m.

  • g = 10 m/s2

Resolución

Para resolver esta cuestión basta con aplicar la ecuación de la posición en caída libre y despejar el tiempo cuando el vaso se encuentra en la posición y = 0 m, es decir, cuando ha llegado al suelo:

Cuestión b)
Datos

  • H = 1.5 m

Cuando llegue al suelo y = 0 m.

  • g = 10 m/s2

Tiempo que tarda en caer al suelo t = 0.55 s

Resolución

Ya que conocemos el tiempo que tarda en caer al suelo, basta con aplicar la ecuación de la velocidad para ese instante:

Lanzamiento vertical

El lanzamiento vertical es un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en el que se lanza un cuerpo verticalmente con cierta velocidad inicial desde cierta altura y no encuentra resistencia alguna en su camino. En la superficie de la Tierra, la aceleración de la gravedad se puede considerar constante, dirigida hacia abajo, se designa por la letra g y su valor es de 9.8 m/s2. Para estudiar el movimiento de lanzamiento vertical normalmente utilizaremos un sistema de referencia cuyo origen de coordenadas se encuentra en el pie de la vertical del punto desde el que lanzamos el cuerpo y consideraremos el sentido positivo del eje y apuntando hacia arriba. Podemos distinguir dos casos según el sistema de referencia considerado:

Lanzamos el cuerpo hacia arriba y por tanto velocidad inicial positiva (v0>0). En este caso las ecuaciones del lanzamiento vertical hacia arriba son:

 

Lanzamos el cuerpo hacia abajo y por tanto velocidad inicial negativa (v0<0). En este caso las ecuaciones del lanzamiento vertical hacia abajo son:


Donde:

  • y: La posición final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro (m)
  • v, v0: La velocidad final e inicial del cuerpo respectivamente. Su unidad en el Sistema Internacional (S.I.) es el metro  (m/s)
  • a: La aceleración del cuerpo durante el movimiento. Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2).
  • t: Intervalo de tiempo durante el cual se produce el movimiento. Su unidad en el Sistema Internacional (S.I.) es el segundo (s)
  • H: La altura desde la que se lanza el cuerpo. Se trata de una medida de longitud y por tanto se mide en metros.
  • g: El valor de la aceleración de la gravedad que, en la superficie terrestre puede considerarse igual a 9.8 m/s2
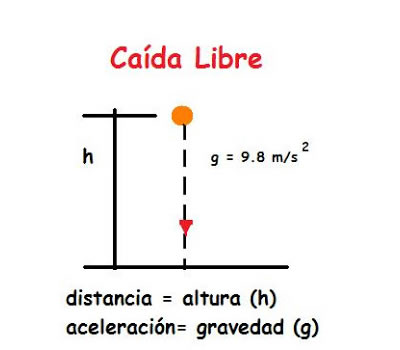Caída libre de los cuerpos Caída libre de los cuerpos
La caída libre es un caso particular del movimiento rectilíneo uniformemente acelerado, es cuando un cuerpo se le deja caer libremente en la cercanía de la superficie del planeta. Un cuerpo que se deja caer en el vacío, se desplaza en linea recta vertical con una aceleración constante, la cual se conoce como gravedad (g), lo que produce que el módulo de la velocidad aumente uniformemente en el transcurso de su caída.



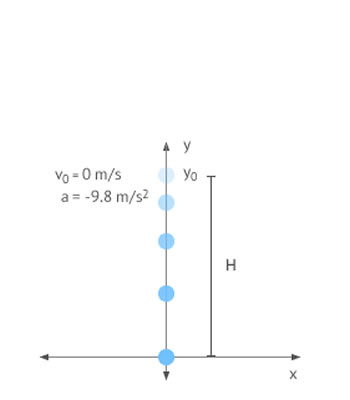Sistema de referencia en caida libre Sistema de referencia en caida libre
A la hora de resolver este tipo de problemas es común utilizar un sistema de referencia como el de la figura. El cuerpo siempre se encuentra sobre el eje Y positivo, e inicialmente su posición es Y0 = H y su velocidad es 0 m/s (ya que parte de reposo) y su aceleración es constante e igual a la gravedad pero con signo negativo ya la tendencia del movimiento es contrario el sentido del eje y. Hay que tener en cuenta que los valores de velocidad obtenidos también son negativos.



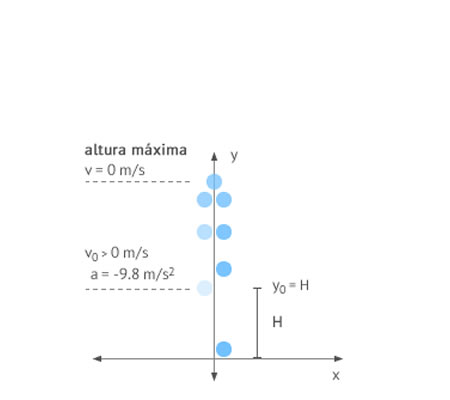Lanzamiento Vertical hacia Arriba Lanzamiento Vertical hacia Arriba
El cuerpo se lanza hacia arriba desde una altura H con una velocidad mayor que 0. A medida que asciende su velocidad va descendiendo hasta que llega a 0 en su altura máxima. Desde ese momento su velocidad es negativa y comienza a descender.



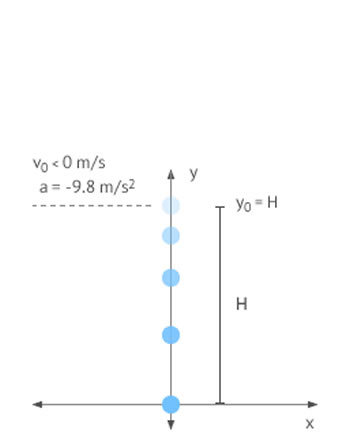Lanzamiento Vertical hacia Abajo Lanzamiento Vertical hacia Abajo
El cuerpo se lanza hacia abajo desde una altura Hy con una velocidad menor que 0 que se mantendrá negativa durante todo el recorrido. Talleres de ciencias naturales Caída libre y lanzamiento vertical.