La densidad y su medida
Los cuerpos que tienen idéntico volumen pueden poseer sin embargo masas diferentes , entoces como diferenciamos uno de otro definimos una nueva magnitud que lo refleje y es la densidad.
La densidad es el grado de compactación de la masa de materia. Cuanto más compactada esté la masa en relación con la cantidad de volumen que ocupa la materia, mayor será su densidad. La densidad es un concepto básico y fundamental en física e ingeniería. Además, tiene una fuerte relación con la masa de un objeto. La densidad la podemos definir como la propiedad que tiene la materia, ya sean sólidos, líquidos o gases, para comprimirse en un espacio determinado, la cantidad de masa por unidad de volumen.
En física la densidad de los cuerpos es la fuerza que tienen sus propias moléculas en comprimirse dentro de un objeto, ya sea líquido, sólido o gaseoso. Pero esta densidad puede variar en función de la materia de la que está formado el cuerpo, excepto los sólidos. Los cuerpos sólidos no pueden cambiar de densidad.
Existen dos tipos principales de densidades, como son la absoluta y densidad relativa. Vamos a ver en que consiste cada una y cual es su formulación.
- Densidad Abosluta Es la relación entre la masa y el volumen, corresponde a todo lo expuesto anteriormente. El resultado de dividir la masa entre el volumen se mide en kg/m³ ó gr/cm³.
- Densidad Relativa Para sólidos y líquidos la densidad relativa es la relación entre la densidad absoluta de un objeto y la densidad de referencia del agua destilada, cuya densidad absoluta es de 1.000 kg/m³, o lo que es lo mismo 1 kg/dm³. Los gases tienen una densidad de referencia distinta, con los gases se utiliza la densidad del aire a una presión de 1 atm. y a 0.°C de temperatura.
Unidad de Medida
El sistema más utilizado a nivel mundial es el Sistema Internacional de Unidades (S.I.), dejando relegado el sistema sajón a países de habla inglesa.
Volumen
Ya hemos visto que es la densidad y como hemos podido comprobar, es un concepto o término asociado a la física. Si trasladamos los conceptos a la geometría o a las matemáticas y estaremos hablando del volumen.
Para calcular las densidades de los cuerpos, necesariamente tenemos que recurrir a las matemáticas, puesto que necesitamos conocer el volumen del cuerpo. Recordemos su fórmula d=m/v.
Tanto en física como en geometría, tenemos que utilizar el término dimensión, formado por ancho, alto y largo. Existiendo tres dimensiones. La diferencia entre una, dos o tres dimensiones son muy evidentes y fáciles de comprender.
- Una dimensión es sólo una línea = Largo.
- Dos dimensiones sería un plano = Alto x Ancho,
- Tres dimensiones sería un cuerpo = Alto x Ancho x Largo.
Calculo de volumen alguna de figuras regulares
Esta característica tridimensional hace que los cuerpos ocupen un lugar en el espacio, y es a ese espacio que ocupa un cuerpo a lo que denominamos volumen. Existen distintos tipos de volúmenes en geometria, y distintas fórmulas para calcularlo como son:
- Cilindro: Para calcular el volumen de un cilindro, debemos multiplicar pi (π), que es un valor fijo 3,1416, por el radio al cuadrado y por la altura (h).
- Esfera: Si queremos calcular el volumen de una esfera, tendremos que aplicar la fórmula de 4/3 multiplicado por el valor fijo de pi, 3.1416 y multiplicado por el radio al cubo.
- Cono: El volumen del cono se calcula multiplicando pi por el radio al cuadrado y por la altura, el resultado se dividirá entre tres y así obtendremos el volumen.
- Paralelepípedo. Para obtener el volumen un paralelepípedo debemos aplicar la fórmula, ancho multiplicado por el alto y multiplicado por el largo.
Calculo del volumen de un cuerpo irregular
Para medir la densidad de un cuerpo es necesario conocer su masa y su volumen, si el cuerpo es irregular, no podemos calcular su volumen de forma directa. Pero podemos calcularlo indirectamente aplicando el principio de Arquímedes.
"Todo cuerpo sumergido en un fluido experimenta un empuje igual al peso del volumen de líquido desalojado"
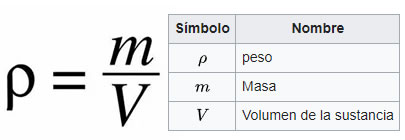 Fórmula de la densidad absoluta
Fórmula de la densidad absoluta Fórmula de la densidad relativa
Fórmula de la densidad relativa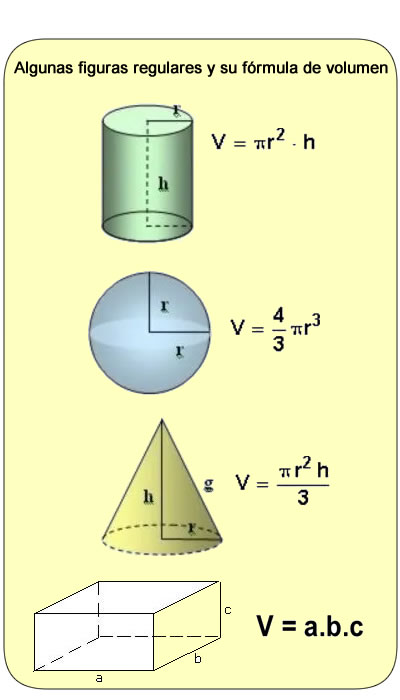
 Un cilindro graduado que contiene varias sustancias químicas líquidas de colores con diferentes densidad
Un cilindro graduado que contiene varias sustancias químicas líquidas de colores con diferentes densidad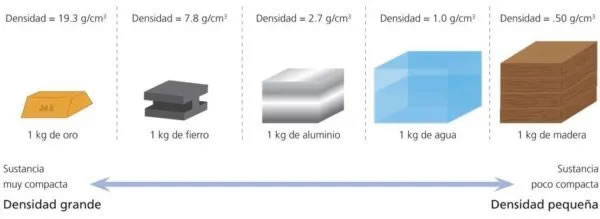 Densidas de diversos materiales
Densidas de diversos materiales